When describing the amplitudes of electronic devices, terms such as “volts RMS” or “amperes RMS” are used. The RMS (root mean square) of a sine wave produces the same “heating effect” as an equivalent DC voltage level. (i.e. 5 VAC RMS = 5 VDC). Since a given AC RMS amplitude is equal to the same “DC heating level” the term is useful for describing amplitudes of irregular shaped or distorted current or voltage waveforms. Two waveforms with different shapes but a similar RMS value will produce the same amount of heat. Valhalla power analyzers directly measure and display the True RMS voltage and current levels for a wide variety of loads, sources and power supplies. The RMS voltage (E rms) may also be shown to be comprised of the following components:

The RMS, Average and Peak amplitude values for a sinewave have a mathematically constant relationship.
| To Convert | To | Multiply ByMultiply By |
|---|---|---|
| RMS | Peak | 1.414 |
| RMS | Average | 0.900 |
| Average | RMS | 1.111 |
| Average | Peak | 1.571 |
| Peak | RMS | 0.707 |
| Peak | Average | 0.637 |
Examine the relationship between current and voltage play in defining a power or watts measurement.
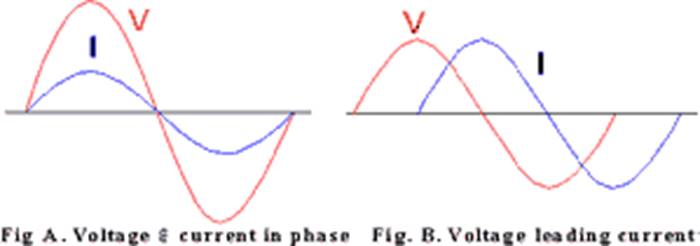
In an AC power measurement, the true power (P) is the product of the voltage (E) and current (I) modified by power factor which is the cosine of the phase shift angle between the voltage and current. For Sine wave loads: P = EI cosθ or True Watts = Volts x Amps x cosθ With a pure resistive load, both the current and voltage are in phase, and the phase shift angle θ is 0 degrees. If θ = 0° = 1 (unity) = P.F. As loads vary from pure inductive through resistive to capacitive, the phase angle varies from – 90° to 0° to +90° and the power factor varies from zero to unity. With an ideal resistive load, the sinusoidal current and voltage are in phase (angle = 0°), the cosine is 1 and the true power (watts) will be the voltage times the current.
